第15章 竜巻回転原子モデルの解釈
本章は、「およよと驚く毎日」様の竜巻回転原子モデルの派生物理に関するものである。 本仮想実験では「およよと驚く毎日」様の竜巻回転原子モデルの概念を引き継いでいるが、解釈は独自のものとなっているので、元のモデルの詳細については以下をご覧下さい。
およよと驚く毎日(モデルを変えれば、原子の謎は全て解けるー質量・万有引力から反重力まで)
【竜巻回転原子の生成】
水素原子の生成初期においては、電子がクーロン力によって陽子に接近し、すれ違っては遠ざかりことを繰り返すことで不規則な球状軌道を描く。
クーロン力が接近とすれ違いの速度とその後の球状軌道を形成するため、如何なる電子と陽子のペアも球状軌道の位置やエネルギーは一定の範囲に収まる。
竜巻回転を維持する仕組みを以下に示す。
電子と陽子が偶々同時に左回転(又は右回転)の竜巻回転になると、磁場の流れも同じ回転方向となり、お互いが相乗効果となり、竜巻回転を包み込んで発生する。(下図は左回転の例)
しかし、電子と陽子が竜巻回転で発生する磁場は、磁気双極子のN極とS局の極性が逆向きのため、内側では打ち消し合い磁場を弱め、外側では距離があるため打ち消しが発生せず強い磁場のままとなる。
この磁場の強さの違いにより電子と陽子にはローレンツ力による向心力が発生し、クーロン力、遠心力とのつり合いが取られ、その結果、竜巻回転が形成し安定する。
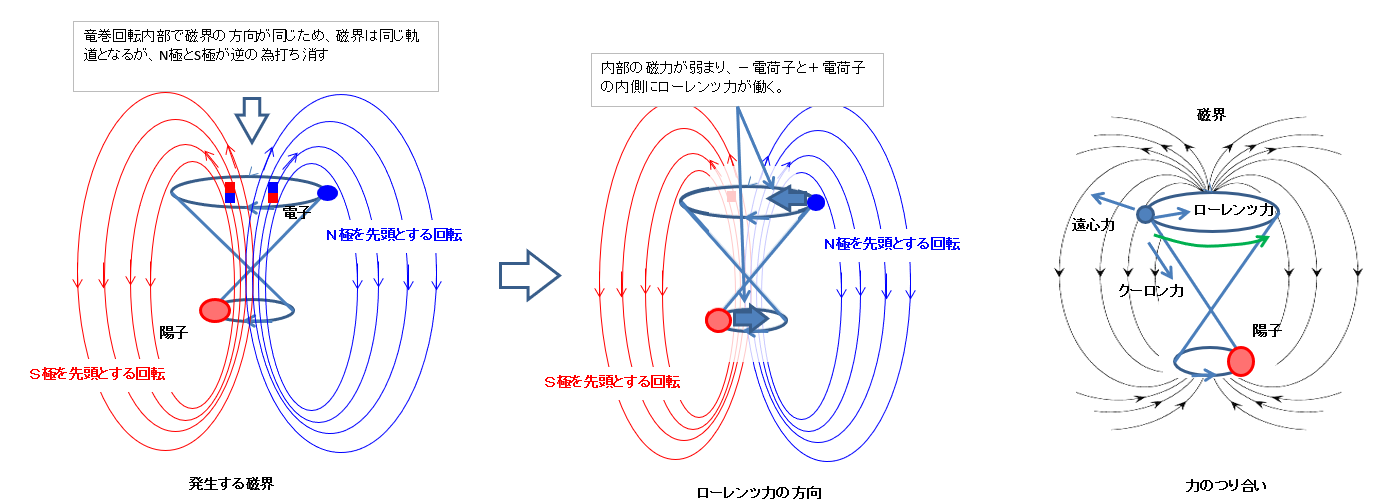
すなわち、原子の竜巻回転は、電子-陽子間のクーロン力、ローレンツ力による向心力、電子(陽子)の回転に伴う遠心力、この3つが釣り合うことで竜巻回転が維持される。
【竜巻回転原子の段(周期律表の族)】
竜巻回転原子モデルは、砂時計のような形状をした原子モデルで、一方の極に電子、反対の極に陽子と中性子が回転しており、その電子側の回転を上から見ると階段状のドーナッツ構造となっている。
元素の周期律表の横軸(族)の元素の数は2,6,10,14という等差数列で増加しているが、この数列は竜巻回転の各段のドーナッツ部の面積の2倍すなわち(2n-1)×2となっており、一つの電子(反対側に陽子・中性子)がこの面積の1単位を占有することで、全ての電子の電場の条件が同じになっている。
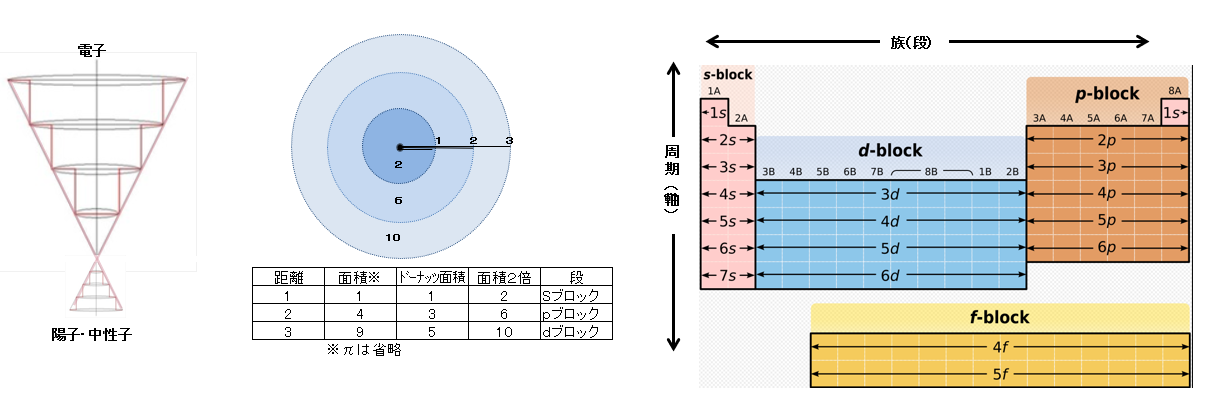
ドーナッツ部の面積が2倍となっているのは、竜巻回転に対する質量バランス、電子内の電荷スピンによる電場バランスが原因であろう。 陽子と中性子は狭い空間に交互に配置される。これは陽子間の反発力を抑える強い力(湯川博士の核力)が「陽子-陽子間では働かず、陽子-中性子-陽子の間でのみ働く」為である。
竜巻回転がドーナッツ構造で安定となる理由は、前述した磁力線によるもので、中心部分の網掛け部は2つの電子・陽子対による磁力線、2番目のドーナッツ部の網掛けは6つの電子・陽子対による磁力線を示し、そのすべての磁力線は最外殻ドーナッツ円の外を通っている。 従って、各々のドーナッツの磁力線の方向は同一であり、そのドーナッツの境界部位を電子と陽子が回っている。 この磁力線により包み込み、ペアを組んでいる電子と陽子を竜巻回転に拘束する。
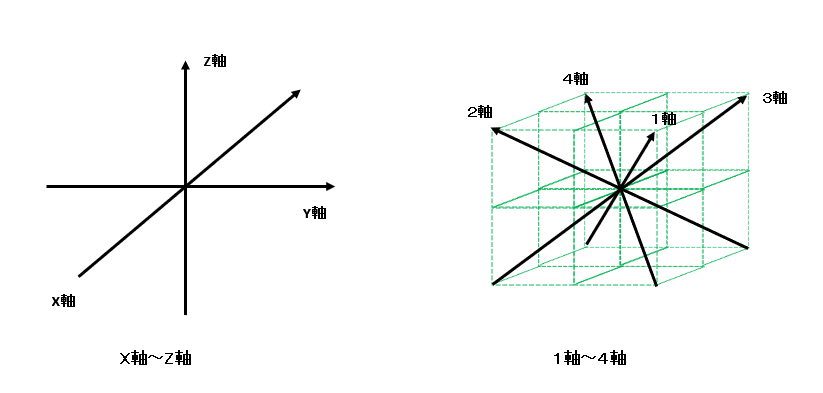
【竜巻回転原子の軸(周期律表の周期)】
次に、周期律表の縦軸(周期)、竜巻回転の軸について述べる。
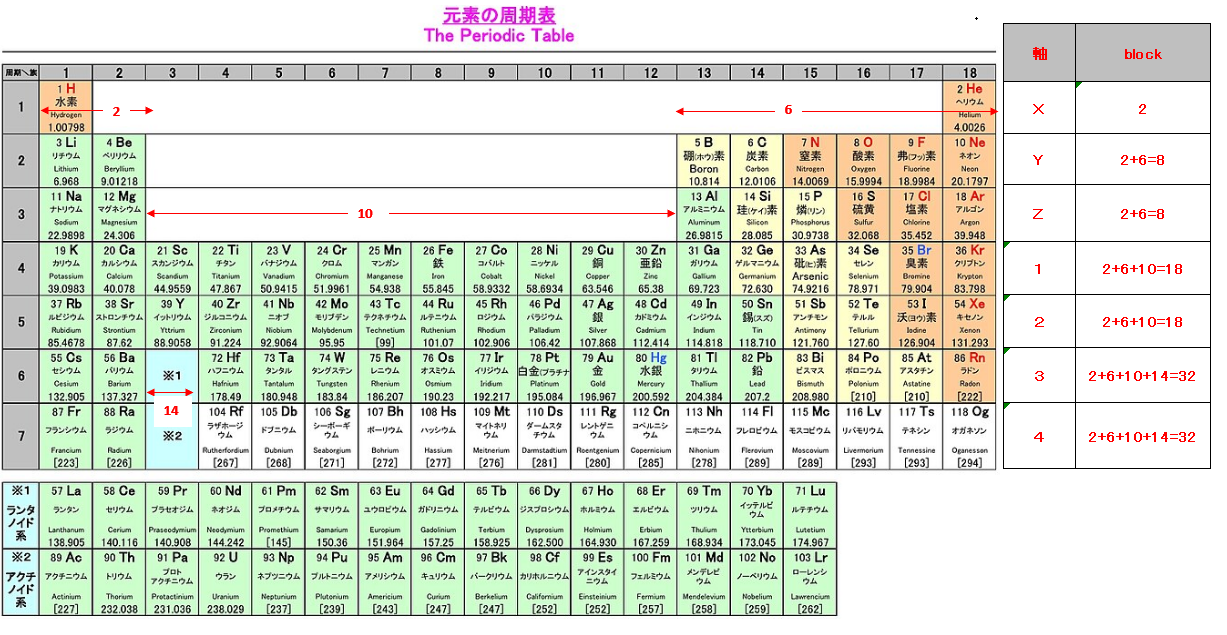
標準原子核モデルにおける、周期律表とエネルギー遷移殻とblockの関係を以下に示す。
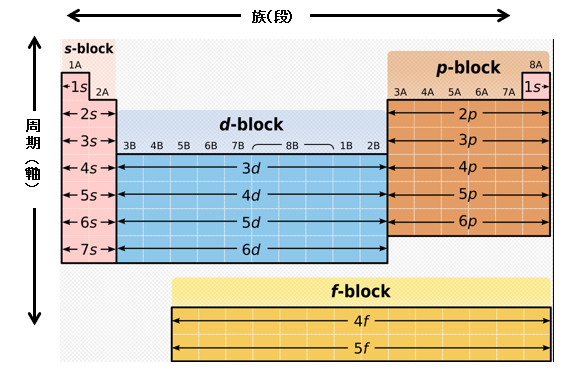

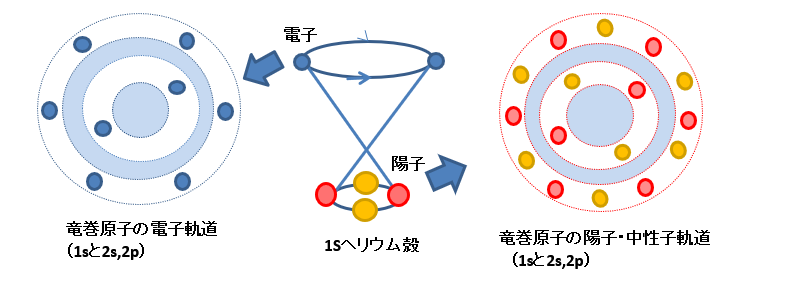
竜巻回転はまずX軸上にK殻(1s)が配置され、一方向に電子が、反対方向に陽子と中性子が配置される。
さらに、Y軸にL殻(2s+2p)が、Z軸にM殻(3s+3p+3d)が配置される。
N殻以上はX軸、Y軸、Z軸の各軸によって分割される8つの立方体の対角方向の空間に、新たな1軸~4軸が出来、Ⅹ軸~4軸まで合計7つの竜巻回転軸が生成される。
新たな1軸~4軸は同型の空間の為、生成される軌道もN殻(4s+4p+4d+4f)と同型の軌道となる。
Ⅹ軸の竜巻回転原子軌道が最初に中央に近い空間を占有すると、これに押しのけられ、次のY軸の竜巻回転原子軌道は中央から少し離れた軌道となる。
軌道が遠くなると電荷の強さは弱くなるため、より大きな空間が必要となり、大きな竜巻回転軌道を取り減少する電荷のエネルギーを補う。
軸が増える都度に、竜巻回転原子の軌道は陽子から離れて、より大きな空間が必要になる。
電子側と真逆の軸の方向には、陽子・中性子が配置されるが、陽子は電子の1836倍の質量を持つため、回転半径は極めて小さくなり回転する円錐も絞られた小さなものとなる。 核分裂は軸の単位での抜き差しが基本であり、分裂の結果発生する端数はよりエネルギーの低い軸と段に再配列され新しい元素になる。
竜巻原子生成時にクーロン力により陽子と電子の衝突が発生しても、陽子と電子が接触した瞬間に電位差がゼロとなりクーロン力も消失、このため対消滅もせず離れていく。 陽子と電子が融合し中性子になるためには恐ろしく巨大なエネルギーが必要だろう。
【竜巻回転原子モデルの妥当性】
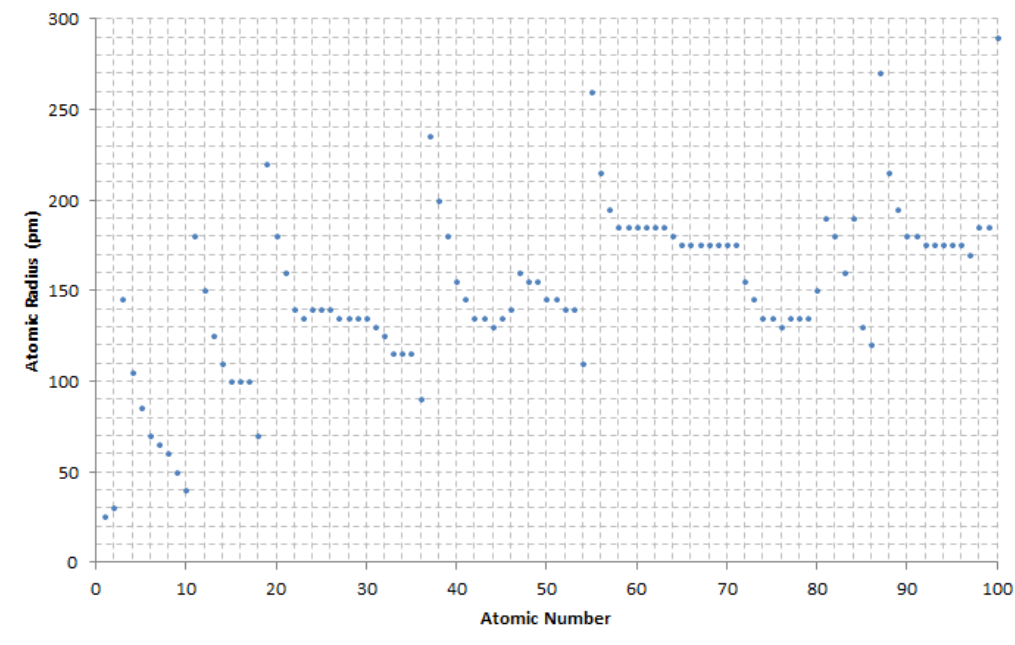
下図は原子半径を示したものであるが、竜巻回転原子の同一軸(同一周期)毎にグループ化され、軸の中では原子数の増加に従って緩やかに下降している。
竜巻回転モデルでは、軸の生成が早いほど軌道が内側となり、新たな軸が追加されると、より遠方に軌道が配置されるため、原子半径は軸生成に合わせ急増する。
原子半径の増加は、Ⅹ軸からZ軸までは急に増え、1軸から4軸の増加は緩やかになる。
これはX~Z軸の増加が、線⇒面⇒空間と大きな変化があるのに対し、1~4軸はX~Z軸で区切られた同一形状の8つの空間(電子・陽子ペアで4つの空間)に制限され、その空間に竜巻回転原子が配置されるためと思われる。
一方各軸の内部は段で構成され順次原子が埋まっていくが、原子数が少ないほどバランスが悪く、原子数が多くなるほど滑らかに回転するため原子半径は縮小する。
なお、前節【竜巻回転原子の軸(周期律表の周期)】の遷移殻(K殻~N殻)と、原子半径による電子数の分類にズレが生じているが、これは、遷移殻の区分けが化学的な性質による分類であるのに対し、原子半径が物理的な距離による分類の違いであろうか?
何れにせよ、原子半径の変化は竜巻回転モデルと一致する。
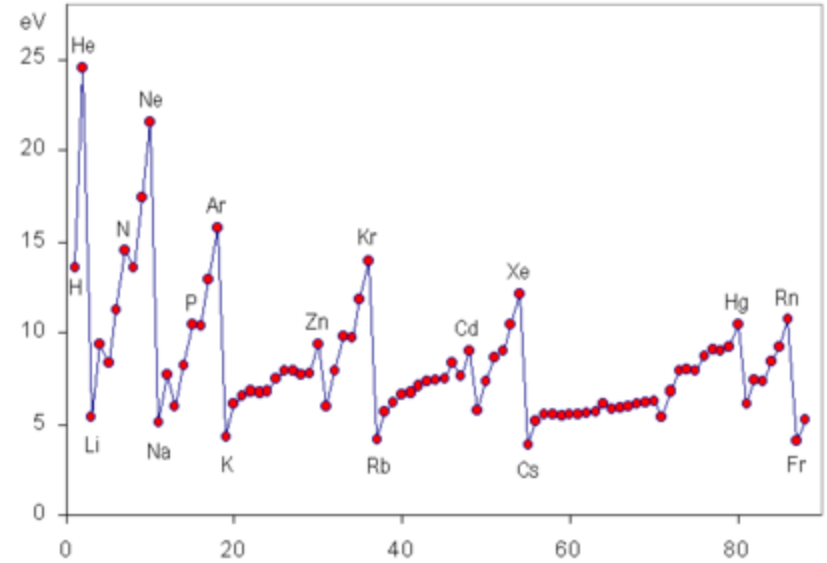
下図はイオン化エネルギーを示したものである。イオン化エネルギーとは原子から電子(最外殻電子イオン)を1つ取り去って陽イオン化するために必要なエネルギーである。
これを見ると、原子半径とイオン化エネルギーは逆相関になっている。
竜巻原子の電子軌道は軸毎に独立しており、ある軸に属する電子を取り去る場合、他の軸の影響を受けないため、全ての軸の影響を受ける原子半径に対し急峻となっている。
段の中で電子が増加すると徐々にエネルギーが増加し、軸が追加されると一気にエネルギーが急減する。
すなわち、イオン化エネルギーの変化も、竜巻回転モデルの存在を示唆している。
【質量差1:1836が一定となる理由】
電子と陽子の質量比は電子:陽子=1:1836であり、その質量差は異常に大きく、また1836倍で一定なのはなぜだろうか?
「5章物質とは何か?」では-電荷子が重力素=1、+電荷子が重力素>1で結合するものと仮定した。 しかし、+電荷子(陽子)が1以上のどの数値となるかは検討しなかったためこれを考察する。
まず、仮に電子:陽子=1:1の場合、竜巻回転原子がどうなるか考える。
この場合、回転は何れの方向にも偏向することがないため重心は球の中心となり、球状軌道で竜巻回転とはならず、1つの陽子と1つの電子のみが軌道を取る。
従ってこのような系では原子構造は生まれない。
次に電子:陽子=1:2を考えてみる。
重心は質量と逆のため、電子側=2、陽子側=1の距離が重心であり、これを重心とした竜巻回転を行う。
しかし、竜巻回転の中心角は大きくなり、竜巻回転の段も軸も構成できず、やはり原子構造は生まれない。
ここで、「竜巻回転原子核の陽子(中性子)を構成する重力素は、空間の重力子を自動的に吸収し質量を増加させ、より多くの段と軸を構成する」ものと仮定する。
多数の段と軸が取れることにより、低いエネルギーで多数の電子軌道が取れ、系としても安定性が増す。
この仮定を行うと、電子:陽子=1:nにおいてnは自動的に増大し、段が多数取られ、軸も複数取ることができる。
nは大きいほど段と軸は沢山取れ安定するが、電荷の大きさによるクーロン力とローレンツ力には力の限界があるため、その最大限界が1836となるのではないだろうか?
【物質と重力素の違い】
物質を構成する電子、陽子・中性子は前述のように、電荷の働きにより電子は重力素1で陽子は重力素1836で安定する。
何らかの方法(粒子加速器等)で電子や陽子・中性子から電荷子を引き剥がすと重力素は「むき出しの重力素」となる。
重力素は物質の中にある状態と物質の外のある状態では動作が異なる。「物質の中の重力素は、電荷子の働きにより空間からの重力子の吸収を行うが、
物質の外にあり電荷子を剥がされた「むき出しの重力素」は、重力子を放出するのみとなり、絶対質量は縮小し続け最終的に重力子となる」
これは、宇宙の始まりにおける原始宇宙が、殆どが重力子で構成される重力子空間である事との整合性も考慮している。
【質量差1:1836の原理】
電子と陽子の質量比が電子:陽子=1:1836になる原理を検討する。
このことから、物質は電荷で安定化していると考えられ、次の仮定を行う。
- 仮定1;重力素は、+電荷で重力子の吸収を開始する。(陽子の質量1836の実現)
- 仮定2;重力素は、-電荷で重力子の吸収を抑制する。(電子の質量1の実現)
- 仮定3;重力子の吸収量は電位差に従う。(重力素の成長の実現)
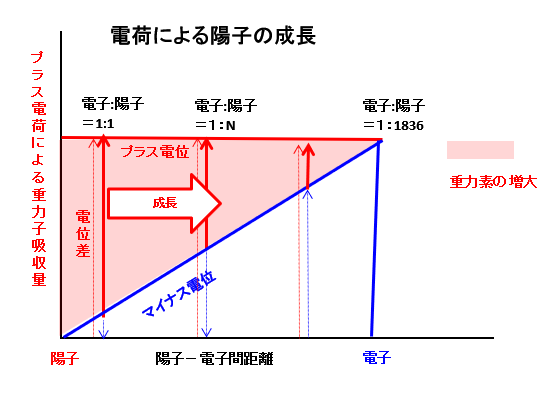
下図は、本仮定による陽子の重力素の成長モデルを示し、左端に陽子、右端に電子があるものとする。
竜巻回転原子の生成初期においては、電子:陽子の質量比はほぼ同じ1:1と考えると、その重心も竜巻回転の中心1:1となる。
この時、電子と陽子の距離は近く、陽子に加わる電位差は大きくなるため、図では左端に位置する。
すると仮定1と仮定3により陽子の重力素の質量は大きく増大し成長する。
陽子の質量が増大し、図の中央の質量N(1<N<1836)となると、竜巻回転の重心位置は陽子:電子=1:Nとなる。
質量Nでは、陽子と電子の距離が離れ電位差は縮小し、その成長率も縮小する。
しかし、現実世界で陽子:電子の質量比は1836:1で安定しているため、その質量比で重力子の吸収は0となるはずであり、これは図の右端に対応し、ここで陽子の質量増加は止まり竜巻回転軌道も1836:1で安定し、同時に、電子は質量1になり安定する。(仮定2)
陽子と電子が質量1836と1で安定化する理由は、空間からの重力子の吸収スピードと、電荷の減少に伴う重力素の蒸発スピードが均衡するためだろう。
以上のことから、電子・陽子が均一な大きさを持つのは、電子・陽子の電荷量が同一なためと考えられる。
「10章重力とは何か?」で検討したように、重力子は重力因子濃度が一定であるため、全て同じ大きさになっている。
重力子が全て同じ大きさを持つため、重力子が分極した光重力子の電荷子も同じ大きさを持つ。電子・陽子の電荷子は光重力子の電荷子が分離したものであるから、電子・陽子の電荷は総て同じ大きさを持つ。
すなわち、電子・陽子・中性子・光(光重力子)・電荷(電荷子)が均一の大きさと強さを持つのは、空間の重力因子濃度が一定のためである。
【鉄は最も安定した物質】
鉄は核融合の最終生成物であり、あらゆる物質の中で最も安定した物質である。
一般論における解釈を以下に示す。
陽子や中性子の質量の最も軽い鉄は、全ての元素の中で,核子間の結びつきが最も強く原子核が安定している。そのため元素が恒星の中で核融合を繰り返し,原子番号が大きく重い元素が作られていっても,鉄よりも重い元素は形成されない。
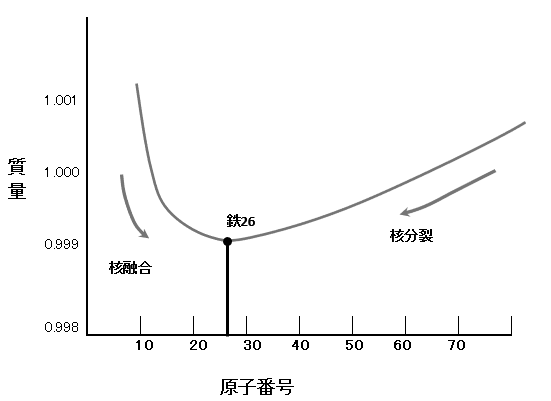
しかし、本仮想物理では相対性理論によるE=MC²を否定しているため、陽子や中性子の、エネルギーの放出による質量の減少は成り立たない。 また、なぜ、鉄が全ての物質の中でボトムとなる曲線になるのだろうか?
以下本仮想物理における解釈を示す。
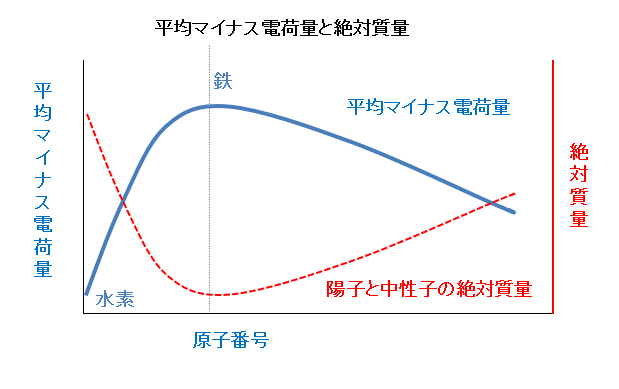
平均-電荷量という量を考える。
平均-電荷量とは、1つの陽子が竜巻回転する電子群から受ける-電荷の強さの平均を示す量である。
水素とヘリウムの場合、電子の半径は水素の方が小さく、従って単独での-電荷量は水素の方が大きいが、ヘリウムは2つの電子があるため、トータルの平均-電荷量は水素(原子番号1)が小さく、ヘリウム(原子番号2)の方が大きくなると考えられる。
ヘリウム以降は、原子番号の増大に伴い電子群から受ける平均-電荷量は増大するが、一定の原子数を超えると電子の軌道がより外部に配置される為、それ以後徐々に減少し始める。
すなわち平均-電荷量は、水素を最低値とし原子数の増加とともに増加するが、ある原子数でピークとなり、さらに原子数が増大すると減少してゆくと推定される(下図青い曲線)。
そのピークとなる原子数が原子番号26の鉄なのだろう。
一方、先の【質量差1:1836の原理】の「電荷による陽子の成長」グラフにて示したように、-電荷の強さは陽子の成長を阻害するため、「陽子と中性子の絶対質量」は「平均-電荷量」と逆相関になり、鉄の陽子が最も軽くなる。(下図赤い破線)
陽子の絶対質量に対し、それを繋ぎとめる強い力は変わらないため、鉄が最も安定した陽子と中性子を持つことになる。
核融合においては、融合のたびに、より安定した陽子と中性子に置き換えられるため、鉄が核融合の最終形態となる。
なお、核融合する際に放出されるエネルギーは、陽子と中性子の絶対質量の放出に伴って不要となった強い力が、光重力子に変換されエネルギーとして放出されたものである。
【E=mC²の見直し】
一般相対性理論では、物質とエネルギーは等価であり、以下の式で現わされる。
E=mC²
しかし、本仮想物理では、光速度不変の原理を否定し、相対性理論を否定しているためE=mC²は成り立たない。 そこで、本仮想物理における物質とエネルギーの関係を考察する。
竜巻回転原子の電子と原子核(陽子・中性子)は、クーロン力、竜巻回転による遠心力、ローレンツ力による向心力により回転を維持しており、常にエネルギーを消費している。
一方、【竜巻回転原子の生成】で説明したように、陽子・中性子の重力素は、生成初期では周囲の空間からの重力子の吸収が放出を上回り、消費するエネルギーに相当する重力子を空間から補充し、最終的に電子・陽子のつり合う均衡点(1:1836)で安定する。
絶対質量Mとは重力素の量であるが、そのエネルギーの開放においては、強い力で結合された重力素と電荷子を光重力子に変換している。
すなわち放出されるエネルギーは絶対質量Mと強い力に比例する。
なお、核融合や核分裂のエネルギーも強い力の開放であり、強い力で拘束された重力素が光重力子のエネルギー(運動+電磁力)に変換され放出されたものと考えられる。
強い力は光速度Cとは無関係であるから、強い力にエネルギー変換定数Sを仮定し、以下の式で核融合や核分裂のエネルギー表すことが出来る。
エネルギー変換定数Sは非常に巨大であろう。
E=M*S (M;絶対質量、S;強い力エネルギー変換定数)
ただし、本式において、「強い力」は「光重力子の運動エネルギー」に変換されるが、重力素の絶対質量Mには変化がない。 膨大に発生した光重力子は、運動エネルギーを消費すると重力子として空間に戻る。
【質量保存の法則】
質量保存の法則とは「閉鎖系においては、時間が経過しても物質の総質量は保たれる。しかし、特殊相対性理論において、質量とエネルギーは等価であると明らかにされたため、質量は厳密には保存しない。さらに非常にエネルギーの高い系では、素粒子物理学における核反応や粒子-反粒子消滅の場合のように、質量の保存は成り立たないことが示されている。」というものである。
以上のように、標準理論では、質量とエネルギーは等価であるため、質量がエネルギーに変換される分、質量は厳密に言うと保存しない。
本仮想物理では、質量とエネルギーは異なるものとしている。
エネルギーとは物質を構成する絶対質量の運動のことで、絶対質量そのものである重力素や重力子は消滅しない。ただし、重力素から重力子への変化、重力子から重力素への変化、
重力素から重力因子の放出、空間の重力因子の吸収、等の変化はする。
核反応や対消滅をしても、核内部の強い力が光重力子の運動エネルギーに変換されるだけで、最終的に絶対質量は重力子として空間に放出されるため消滅はしない。
しかし、前述の【質量差1:1836の原理】にて示したように、陽子は空間からの重力子の吸収と、竜巻回転による回転エネルギーの消費が釣り合って均衡したものであり、重力素の絶対質量は極小の脈動を繰り返している。
従って、重力素(むき出しの重力素)・重力子・重力因子を含まない狭義の物質に限定した世界では、質量保存の法則は成り立たない。
【零点エネルギー(絶対零度)】
絶対零度でも電子は運動しておりエネルギーを持っている。
これを零点エネルギーと言うが、何故絶対零度でもエネルギーをもつのだろうか。
温度とは竜巻回転原子による電子の回転運動である。
原子の竜巻回転は、電荷によるクーロン力、ローレンツ力による向心力、旋回による遠心力のつり合いで回転半径が保たれている。
陽子と電子の電荷子の引き合いによるクーロン力、ローレンツ力は一定であるため、温度による違いは竜巻回転の電子軌道の位置と電子の速度の違いとなって現れる。
高温になると電子軌道は広角で高速となり、低温になると挟角で低速となる。
電子がクーロン力による引力、ローレンツ力による向心力、旋回による遠心力、この3つの力をつり合わせる最小挟角の電子軌道の、最も小さな運動が絶対零度であり、これを下回る軌道では竜巻回転構造を維持できないため、これ以下の運動、すなわち温度は存在しない。
竜巻回転原子構造が維持可能な最低エネルギーが零点エネルギーであり絶対零度である。
【電子雲】
量子力学では電子を雲のように不確定なものとしている。
本竜巻回転原子でも同じように雲のようになっているが、これを以下に説明する。
1つ目は、竜巻回転による軌道の不安定さであり、3次元で旋回する揺れ動くコマの運動からくる不確定さである。
2つめは、旋回する電子の電場が、空間の重力子に分極を起こし、磁気双極子を発生させ電磁波を発生させる。すなわち、旋回移動する電子の周囲には、電磁場が纏いついており、これが雲のように観測される原因となる。
この2つの不確定性が混じり波動関数となる。
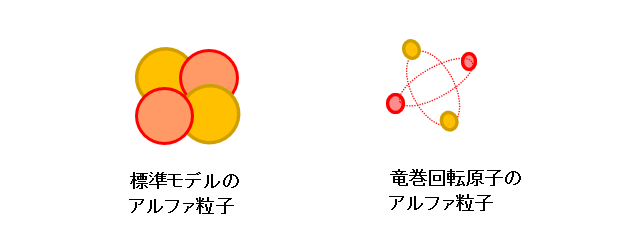
【核分裂とアルファ粒子】
標準原子モデルでは原子核は原子の中央に一体化し存在している。
一方、竜巻回転原子核の陽子と中性子は、竜巻回転により作られる軸と段の軌道上にバラバラに配置されている(下図)。
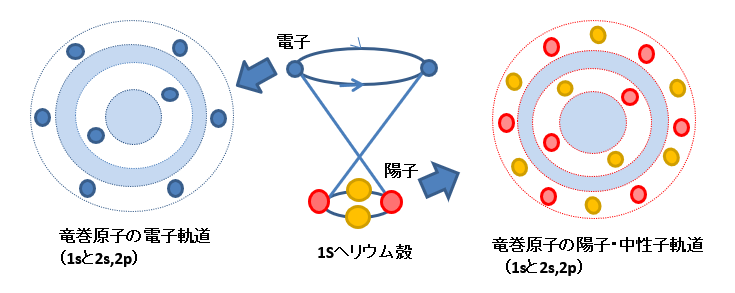
アルファ粒子は核分裂の時に放出されるヘリウム核(陽子2個、中性子2個)である。
標準原子モデルで放出されるアルファ粒子は、陽子2個と中性子2個が接合し一体化した粒子である。
しかし、本竜巻回転原子モデルで放出されるアルファ粒子は、元の原子核がそのまま抜け出したもので、強い力を継続したまま、陽子2個と中性子2個がバラバラにお互いの回りを回転している分散粒子である。(下図)
アルファ粒子は竜巻回転原子のs軌道のヘリウム核であるが、核分裂は軸の単位での抜き差しが基本となっており、電子が剥がされても、ヘリウム核の強い力は暫く維持され、分散原子核として存在する。
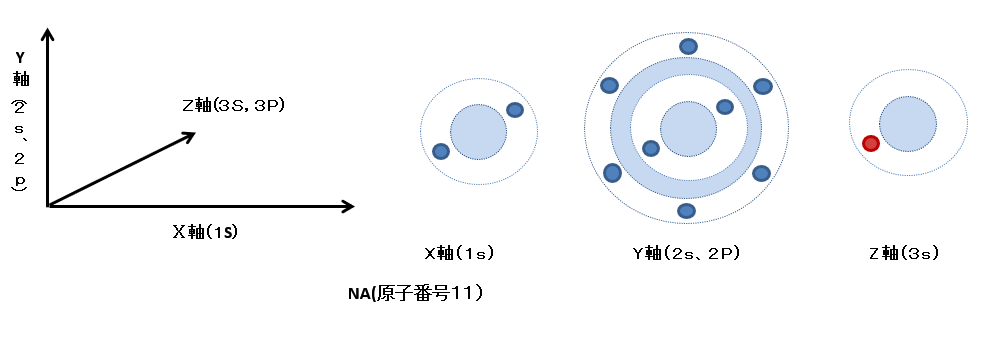
【イオン化】
一般理論のイオン化とは「原子は最外殻の電子数が安定となる閉殻構造(2個、8個、)の電子配置をとる」とされている。しかし、何故閉殻構造で安定となるのだろうか?
竜巻回転モデルでは、電子の座席は、主に対極にある原子核の陽子からの+電荷による電位により決まるが、完全に1:1の関係にあるのではなく、周囲の陽子や電子の影響もうけ、アナログ的なくぼみ(+電位のくぼみ)となっている。

通常、-電荷は、そのくぼみに嵌り、またその-電荷は、周囲の電子と協調しさらに安定化する。
しかし、Na(11)のように最外殻の竜巻回転軌道に電子が一つしかないと、周囲からの陽子や電子による協調がないため、くぼみが浅く平坦になる。
このため、最外殻の電子にエネルギーを与えると、くぼみの電位が振動し、容易に、電子がくぼみから放出され、水素イオンのように陽イオンとなる。
逆に、Cl(17)のように座席が一つ不足している場合は、対局の陽子がなくとも、周囲の陽子や電子により浅いくぼみが形成され、ここに自由電子がはまり込み、陰イオンとなる。
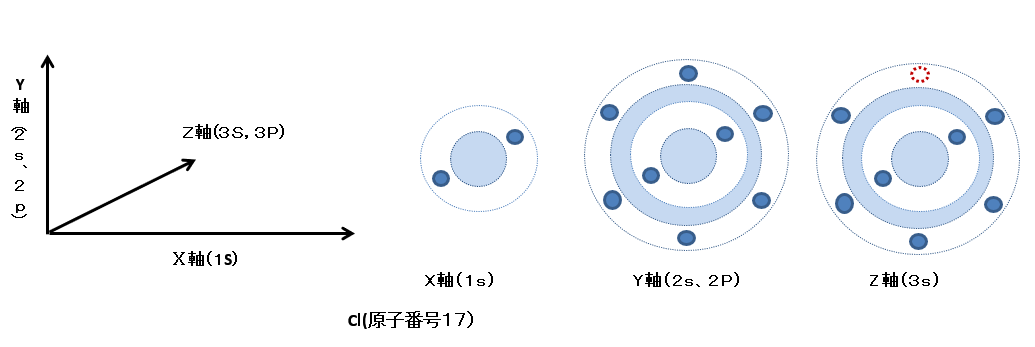
一方、陽子と中性子の原子核は強い力により拘束されており、電荷の力で変化することはない。
【粘性と超流動】
一般論における粘性と超流動
- ・流体における粘性は、分子間力(ファンデルワース力)によるものである。軌道上の電子はいつも均等に配置されるわけではなく、電位が-に傾いたり、+に傾いたりしており、この電位の偏りにより、分子同士の引き合いが発生する。 液体が形を変えようとすると、この分子間力が変わろうとする動きの邪魔をする。 この、抵抗する力が粘性で、液体の粘性がそれぞれに違うのは分子間の引き合う力が違う為である。
- ・超流動とは、極低温において液体の粘性が消失する現象で、「液体が容器の壁をよじ登る」「通常の液体では通り抜けられないような狭い隙間から流れ出る」という現象が起きる。 これは、量子効果が巨視的に現れるボース・アインシュタイン凝縮により発生する。
一般論ではボース・アインシュタイン凝縮が超流動の原因としているが、何故量子レベルの現象が巨視的な世界でも現れるのだろうか?
仮想物理の解釈を以下に示す。
- ・粘性は一般論と同じ分子間力(ファンデルワース力)により発生する。
- ・竜巻回転原子では、電子の軌道は軸と段で構成され、電子雲は軸の単位で発生し、形状は段、及び段に属する電子の数で変化する。
- ・電子雲の形状が複雑になるほど、電子の配置の偏りが発生しやすく、電子の数が多い程、その影響も大きく出る。この電位の偏りにより、分子同士の引き合いが発生し粘性が発生する。
- ・粘性は電子雲が複雑で変動が大きいほど強く発生する。一方、超流動は電子雲が単純で、極低温において電子雲が極限まで安定すると発生する。
- ・原子は「クーロン力による引力」「竜巻回転による遠心力」「ローレンツ力による向心力」の3つの力のつり合いで運動しており、この運動が物体の温度となる。 しかし、【零点エネルギー】において説明したように、物体を絶対零度近くまで冷却すると、竜巻回転による軌道は最低エネルギーの軌道に落ち着き、運動による変化のない安定な状態でつり合う。従って、絶対零度に近い温度において、電子雲の変動は最小となり、電位の不均衡が消失する。 その結果、分子間力が無くなり粘性が消失し、超流動が発生する。
- ・ヘリウム(4He)は外殻電子数が2個で元々安定した電子雲を持つが、零点エネルギーに近い極低温で最小エネルギーになると、電子雲の変動は最小となり、粘性が消失する。
- ・一方、液体水素は電子が1個しかないため、電子雲は不規則で刻一刻と変化し分子間力もなくならない。 しかし、極限まで零点エネルギーに接近させると、電子雲が安定し超流動が起きる。 すなわち、フェルミ粒子(水素)でも超流動は発生し、ボーズ粒子(ヘリウム)との違いは発生のし易さだけで、絶対零度に近づければどちらも超流動を起こす。
-
・比熱測定で液体ヘリウムを減圧冷却し、温度を下げて行くと、下図のように、一定の割合で比熱が低下した後、Tλ(2.17°K)で急に上昇し、それから急降下し超流動を起こす。
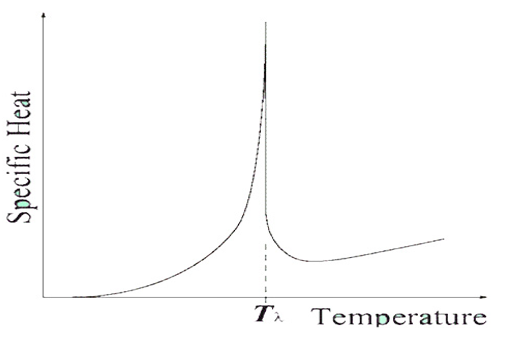
粘性は分子間力によるもので、電子雲が複雑なほど発生しやすい。
温度を下げると、電子雲の運動変化は少なくなり、これに伴って粘性も下がる。
比熱は熱による運動のし難さであるから、粘性が高い程比熱は高く、粘性が下がると比熱も下がるはずであるが、Tλで比熱が急に上がるのは、粘性が急に高まった為と考えられる。 粘性は電子雲の複雑さであるから、Tλまでの電子雲の形状が、Tλで相変移を起こし新しい形状となり、この変移による変動で粘性が高まり比熱が高まったと推測できる。 Tλ近辺で鋭いピークとなるのは、2種類の電子雲の形状を行ったり来たりして一方に定まらない為、電子雲が複雑化するためだろう。
さらに温度を下げ、電子雲が新しい形状に落ち着くと、急速に粘性が落ち比熱も下がる。そして粘性が急速になくなり超流動を起こす。
「液体が容器の壁をよじ登る」という超流動特有の現象は、液体ヘリウムの粘性が低下する一方、容器との間のファンデルワース力はそのまま残り、その2つの力が逆転した為に発生した現象と考えられる。
【電子の遷移エネルギー(バルマーの公式)】
電子がm軌道からn軌道に遷移する時に光が放出され、その振動数を示したものがバルマーの公式である。
ν=1/λ=R(1/m²-1/n²);Rはリュードベリ定数
この公式を竜巻回転原子モデルで考えてみる。
竜巻回転電子のエネルギーは円錐の中心の陽子から距離の二乗に反比例する。
(厳密には電子:陽子=1:1836の陽子の竜巻回転の考慮が必要だが、比率が大きい為無視する)
従って、m段からn段に遷移する時、は1/m²-1/n²の差に比例するエネルギーが放出される。
仮にエネルギー変換定数をSとすると、E=S(1/m²-1/n²)となる。
光のエネルギーEは周波数νに比例し、E=hν(hプランク定数、ν周波数)で表されるため、E=hν=S(1/m²-1/n²)となる。
両辺をhで除算しS/hをRで置き換える。
ν=S/h*(1/m²-1/n²)=R(1/m²-1/n²);
すなわち、竜巻回転原子の構造から、容易にバルマーの公式が導かれる。
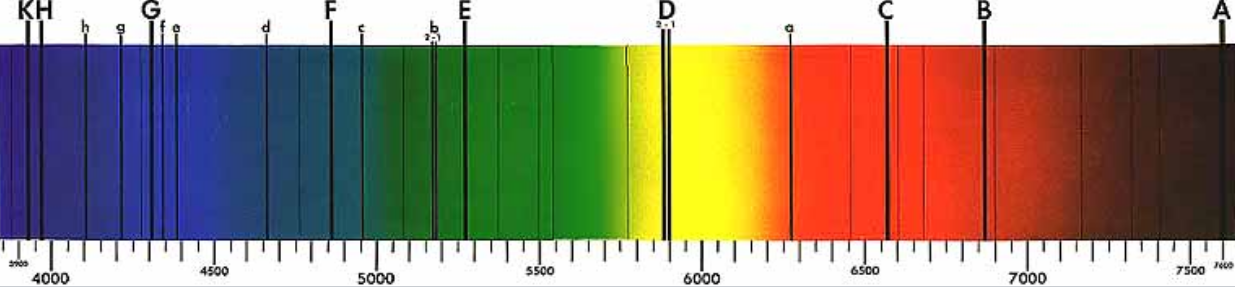
【フラウンホーファー線】
フラウンホーファー線とは、太陽光の可視光の連続スペクトルの中に見られる暗線のことで、太陽の高温部で発生した光が、太陽の低温部や地球大気の各種元素によって、特定の波長が吸収されることで発生する。
ところで、竜巻回転原子の渦巻回転軌道は、エネルギーの低い内周から生成され、順次エネルギーの高い外周へと、原子番号の増加とともに竜巻の段が自動的に追加されている。
すなわち、竜巻回転原子においては、次に追加される段が、電場の変異などから、予め定められているはずである。
そこで、「電子がある軌道で周回している場合、次の軌道への電位差を電子の波動に変換し、同様に2番目・3番目以降の電位差も波動に変換し、その全ての波動が電子の運動に合成される」ものと仮定する。
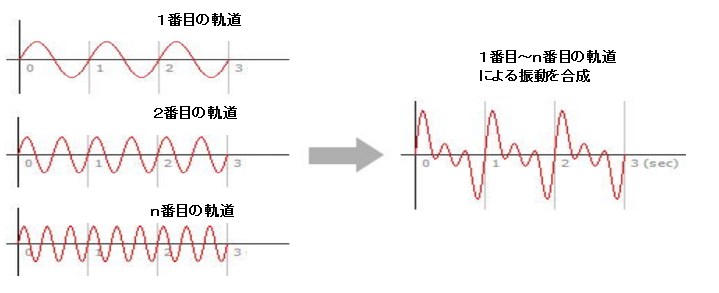
電子に照射された太陽光の波長と、電子の合成波長の中の一つの波長が一致するとき、電子は光のエネルギーを吸収し、それに対応する軌道に遷移する。 この遷移により失われたエネルギーが暗線となる。
【水素スペクトル系列】
原子のスペクトル線は電子のエネルギー準位間の遷移に伴う吸収・放出により説明される。
このうち最も簡単な元素である水素のスペクトルを分析したところ、リュードベリの式(バルマーの公式と同意)の波長に従うことが判明した。
水素のスペクトル線は、最内部n=1軌道の紫外線波長(Lyman Series)、n=2軌道の可視光波長(Balmer Series)、n=3軌道の紫外線波長(Paschen Series)の複数スペクトルに系列化される。
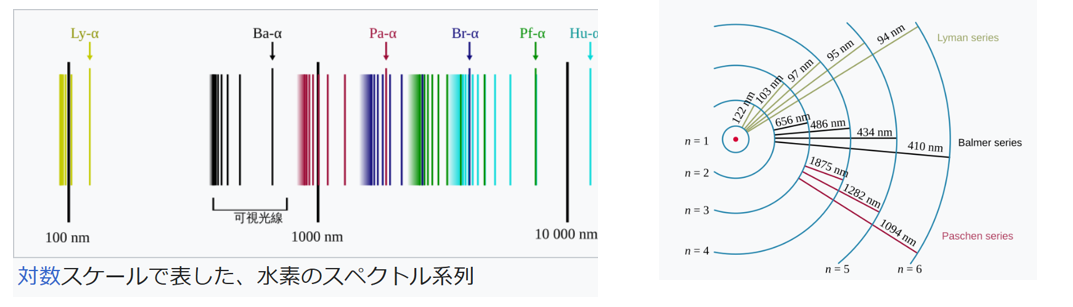
竜巻回転水素原子では通常n=1の竜巻軌道に電子が存在するが、その電子は次のn=2~m軌道までの電位差を各々の周波数とする波を合成波として纏っている。
太陽光は広範囲の連続した波長をもつ光重力子の群れであるが、個々の光重力子は固有の波長をもつ。
ある光重力子の波長と、電子の合成波の中の一つの波長が一致すると、光重力子は電子に吸収され、そのエネルギーによって電子は対応する軌道に遷移し、光重力子が抜けた分が暗線としてスペクトルに現れる。
さまざまな波長の光重力子が電子と衝突し、波長が一致した光重力子のエネルギーが吸収され、この繰り返しにより、n=1軌道からの紫外線波長のスペクトル系列Lyman Seriesが現れる。
n=2軌道に遷移した電子は、その軌道で、次のn=3~mについて同じように軌道差による合成波を纏い、この電子が同じ波長の光重力子を吸収するため、可視光波長のスペクトル系列Balmer Seriesが現れる。
同様に、n=3軌道に遷移した電子により赤外線波長のスペクトル系列Paschen Seriesが現れる。
遷移先から元の軌道に戻ると吸収したエネルギーを光として再放出する。
水素スペクトル系列は、竜巻回転原子が段と軸を新規に構成する際の順番を示し、このエネルギーが低い順番から構成されるのだろう。
【竜巻回転原子の回転エネルギーの維持】
竜巻回転原子の陽子・中性子・電子はお互いの回りを、電磁波を発生しながら回転しているため、何れエネルギーを消耗し回転が止まってしまう。
従って、何らかの方法で消耗するエネルギーが補給されているものと考えられる。
竜巻回転原子核の陽子と中性子は、空間の重力子を吸収し、1,836倍の質量に成長し均衡したものである。
吸収された重力子の一部は、光重力子に分極され、さらにこれが+電荷子と-電荷子に分離され、回転を維持するエネルギーとなっているものと思われる。
この一連の仕組みを「光重力子変換システム」と呼ぶ。
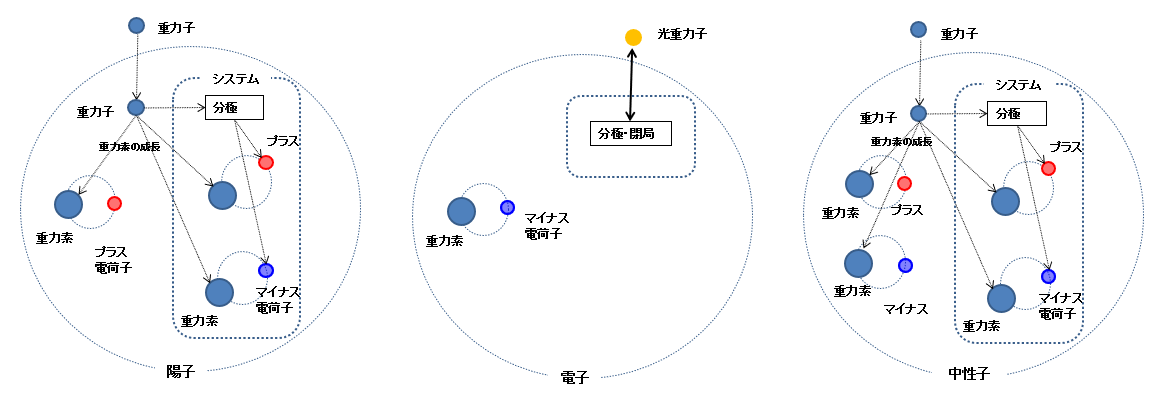
1.陽子
陽子は、空間から重力子を取りこみ、これを分極し光重力子とする。さらに光重力子は+電荷子と-電荷子に分離される。 この重力子、+電荷子、-電荷子を元に、重力素と+電荷子、重力素と-電荷子のペアからなる、「光重力子変換システム」が構成され、このシステムが陽子の質量の維持と、消費される竜巻回転エネルギーの供給を行う。 陽子には、元々の重力素と+電荷子のペアがあるため、2組の重力素と+電荷子、1組の重力素と-電荷子の組の合計3組のペアが出来る。このシステムは、標準理論におけるクォークに相当する。
2.電子
電子の軌道遷移では光子の放出と吸収でその軌道の変更がなされる。 電子の質量1に対し、陽子の質量は1836であり、圧倒的に小さいことから、質量が増加する一式の「光重力子変換システム」はない。 しかし、光エネルギーの吸収と放出する機能だけはあり、光重力子の分極と閉極を行い竜巻回転エネルギーを維持している。 従って、電子は、元々の重力素と-電荷子の1組のペアのみから構成される。
3.中性子
中性子の質量は1.67478 x 10-27 kg、陽子の質量は1.67248 x 10-27 kg、と中性子の質量の方が大きい。 このことから、中性子は元々の、重力素と+電荷子、重力素と-電荷子のペアに加え、重力子から作られる1対の「光重力子変換システム」を持ち、この結果、中性子には2組の重力素と+電荷子、2組の重力素と-電荷子の組の合計4組のペアが出来る。
【カシミール効果】
真空に薄い平面金属板を接近させると引き合う力が発生する。
空間に存在する重力子は重力因子の吸収と放出を行い、重力子と重力素の間を行き来している。すなわち重力子は低エネルギーではあるが脈動をしており、真空中では金属板と均等に衝突し全方向に等価な圧力を発生している。
この状態で2枚の金属板を限りなく接近させると、2枚の金属板の間の重力子の数が少なくなり衝突が減る。
この差により発生するのがカシミール効果である。
