因子とは粒子間で力を介在する超粒子であり、因子そのものに機能はなく、これを受信した重力素や重力子がこれを検出し機能を発動させる。
なお、本仮想物理では粒子の末尾に、「素」／「子」／「因子」をつけ区別している。例として重力素、重力子、重力因子である。 この区分けは絶対質量を目安にしており、素＞＞子（≒０）＞＞因子（＝０）としている。
この区分けの場合、電子・陽子・中性子は「素」のグループに属するが、電子・陽子・中性子はあまりに一般化された名称のため、そのまま電子・陽子・中性子を用いている。
（奇怪展界では、標準物理学に相応する粒子があれば、そのまま奇怪展界の粒子名として使用している。具体的には電子、陽子、中性子、磁気双極子である）

素粒子の標準模型を以下に示す。

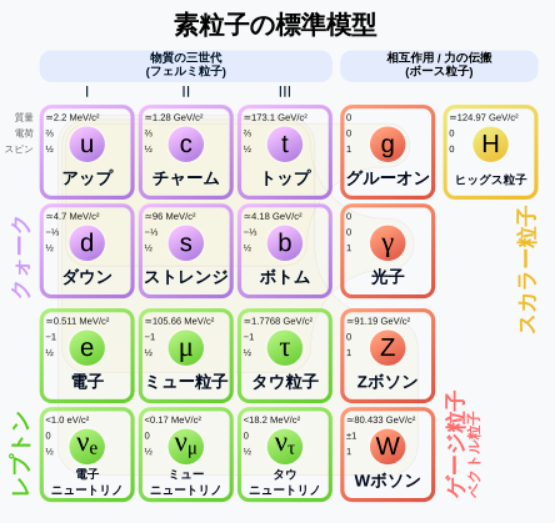
本仮想物理における素粒子模型と標準模型の対比を下図に示す。
標準模型のフェルミ粒子に対応するのは重力素のみである。 ボーズ粒子は重力子を基本に、重力子から分化した粒子が対応し、ヒッグス粒子に対応するのは重力因子である。
電子と電子ニュートリノは本仮想物理では重力素に対応しており、電子は－電荷子と重力素（１Ｇ０）の結合粒子、ニュートリノは重力素（１Ｇ０）の単独粒子である。
また、クオークは重力素の集合状態の違いである。（詳細は第１５章　竜巻回転原子モデルの解釈【竜巻回転原子の回転エネルギーの維持】参照）

【重力因子】

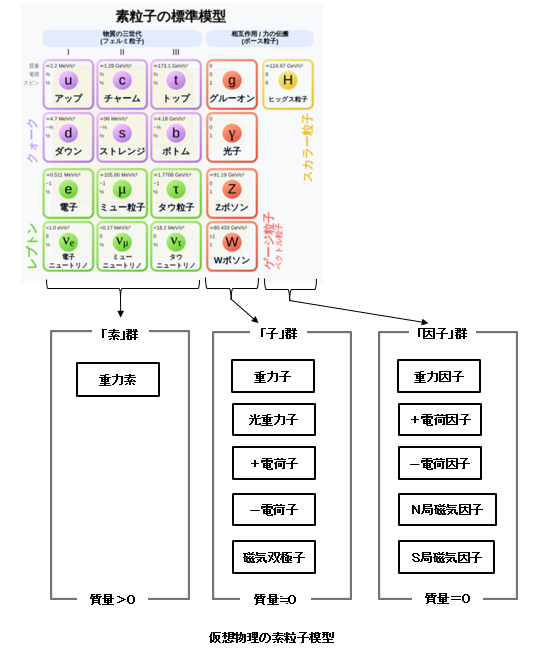
「１０章重力とは何か？」で記載したが、重力因子は図１，図２で示すように、近傍に物質（重力素）がなければ、全方位から均等に降り注いでおり、発生する重力はつり合い、トータルの力は発生しない。 このつり合う重力を慣性重力と言い、発生する質量を慣性質量と言う。

一方、図３のように近傍に他の物質がある場合は、その方向からの重力因子が他の方向より大きくなり、引き合う力が発生する。この力をを引力と言い、発生する質量を引力質量と言う。

重力は引き合う力のみで排斥力が存在しない。 物質から出た重力因子は何者にも引き寄せられない。
また、重力因子は物質や重力子に衝突しないかぎり進行を妨げるものはなく、重力による慣性抵抗も発生しないため、速度は無限である。
重力素から均等に放出された重力因子は、図４のように無限の彼方に向け一直線につき進む。 重力が他の電荷子や磁気双極子と違い、宇宙規模で影響を及ぼすのはこのためである。

宇宙の彼方で重力異常が発生すると、その影響は宇宙全体に瞬時に到達する。

万有引力の法則は、F＝G＊（M1＊M2）／r＊＊2である。
重力因子は直進するため、相手からの影響は投影面積になり距離の2乗に反比例し、相手と自身の質量の積に比例する。 従って、重力因子モデルと万有引力の法則は矛盾しない。

【電荷因子】

一般理論では「電磁気力の力の粒子は光子で、電磁気力は光子をやり取りすることで伝わる」とされているが、本仮想物理では、光子（光重力子）は電荷が－電荷子と＋電荷子に分極した粒子であるため、力の粒子は光子ではない。

電荷を保有するのは、電子と陽子、及び光重力子（電磁波）の二種類であるが、電荷の発生源は何れも＋電荷子と－電荷子であり、力は電荷子の間でやり取りされる。
そこで、重力と同じく、力を介在する粒子として電荷因子を考え、電荷子には＋と－に対応して＋電荷因子と－電荷因子があるものとすると、この粒子は、重力に影響されないため慣性抵抗が発生せず、無限の速度をもつ粒子となる。
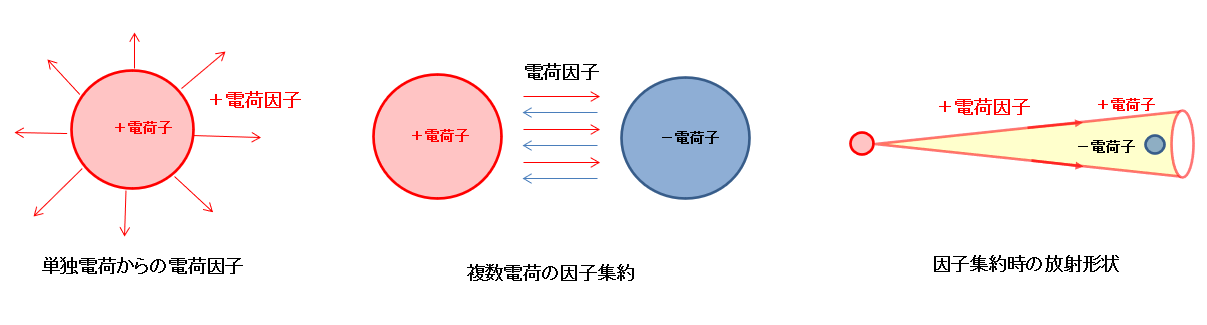
－電荷からは－電荷因子、＋電荷からは＋電荷因子が放出され、受け取った電荷では、自身と異なる電荷因子なら「吸引力」を、同じ電荷因子なら図２のように「反発力」を生成する。

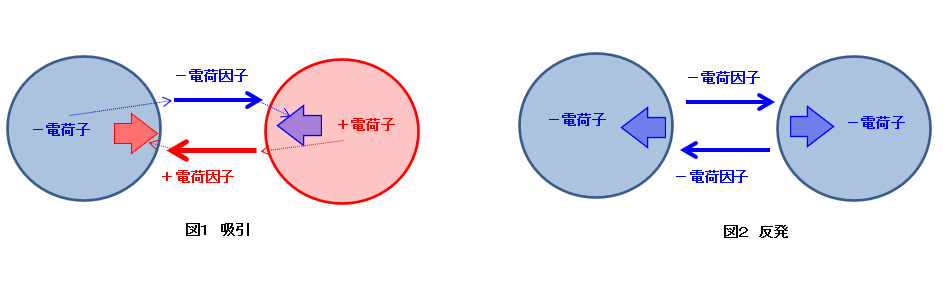
電荷因子は電荷子が単独の場合、均等に外部に放出されるが、２つの電荷子が近隣に存在する場合は、相手の電荷因子を受信すると、それに応じ自身の電荷因子を受信した方向に送り返すものと仮定する。
この状態になると、電荷因子のやり取りが２つの電荷間で繰り返され、電荷因子の殆どが2つの電荷子に独占される状態になるため、この電荷因子の状態を因子集約と呼ぶ。

ここで、クーロンの法則は距離の逆二乗に比例するため、放出される電荷因子はサーチライトのように拡散すると考えられる。（下図）
電荷因子の速度は無限であるが、電荷内での電荷因子の送り返しは有限時間なので、完全なる衝突にはならず、サーチライトのような拡散が発生する。
因子集約によりクーロン力は重力に比べ巨大となる。

固定された2つの＋電荷子と－電荷子の間に、移動する＋電荷子を置いた時、その＋電荷子が移動する全ての軌跡の仮想的な線を電気力線と言うが、因子集約は距離の逆二乗に比例するため電気力線の曲線を描く。

【磁気因子】

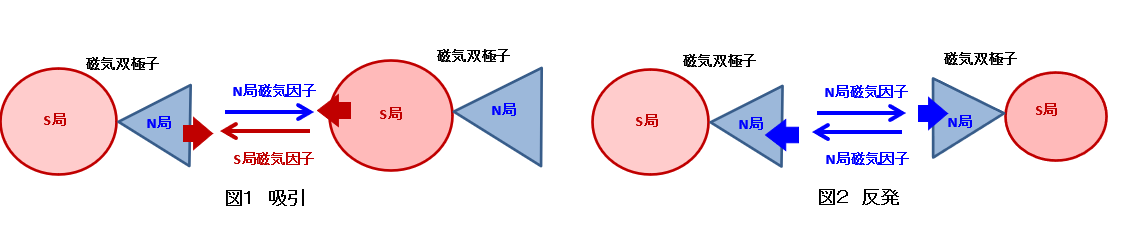
磁気双極子のN局からはN局磁気因子が、S局からはS局磁気因子が放出され、反発力と吸引力を発生させる。
磁気因子も重力に影響されないため慣性抵抗が発生せず、速度は無限である。

磁気双極子が単独で存在する場合、磁気因子は均等に外部に放出されるが、近隣に他の磁気双極子が存在する場合はお互いの磁気因子を交換しあう因子集約が発生する。
因子集約では、相手の磁気双極子に向け磁気因子が放出されるが、全ての磁気因子が相手に衝突するわけでない。
相手の磁気双極子に放出される磁気因子は、サーチライトのように拡散すると考えられ、このため発生する力は距離の逆二乗に比例する。
因子集約により磁気力は重力に比べ巨大となる。

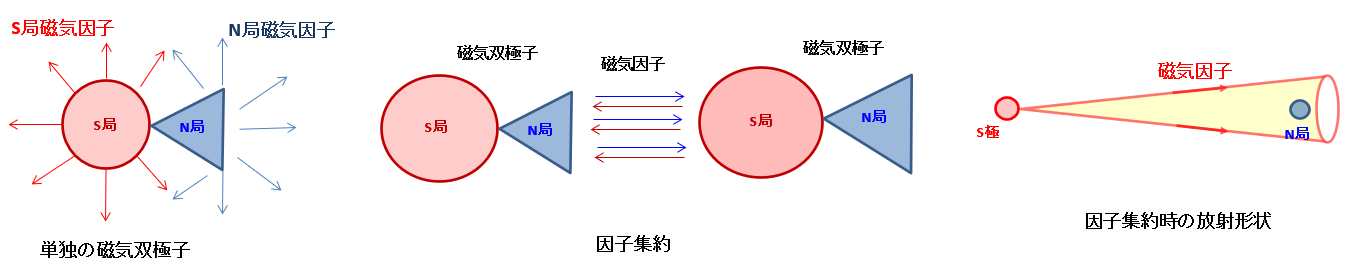
磁石が描く磁力線は、磁気双極子がローレンツ力で回転しながら押し出されたもので、磁気因子が逆二乗に比例することで生成される。

【ローレンツ力と因子】

－電荷子から放出された－電荷因子はN局に対し排斥力を発生させる。 また、N局からもN局磁気因子が放出され－電荷に対し排斥力を発生させる。
＋電荷とS局も同じである。
ローレンツ力は排斥力のみで吸引力は存在しない。
ローレンツ力を伝えるのは電荷因子と磁気因子であり、このいずれも重力には影響されないためローレンツ力の伝達速度は無限である。

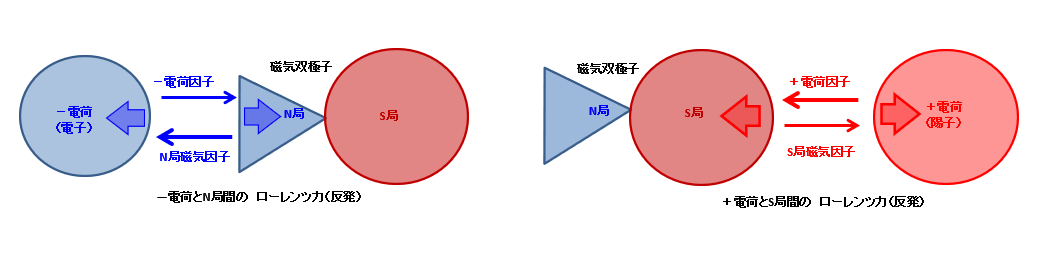
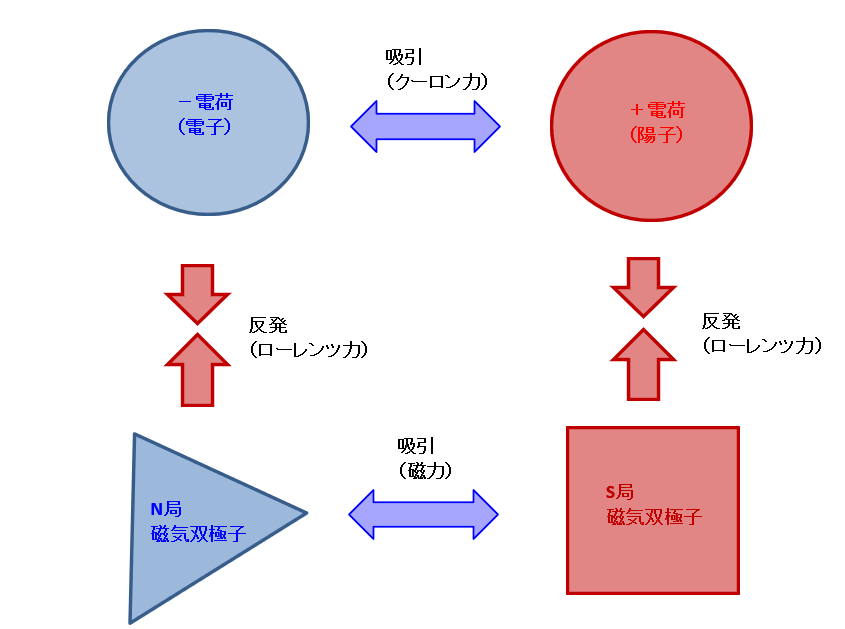
ローレンツ力にも因子集約が発生し、その力は電磁気力と同じく非常に強い。

【量子もつれ、量子テレポーテーション】

因子が複数粒子間でクロス共有した状態。
例えば光のもつれの場合では、ある光子の―電荷子と＋電荷子の間の電荷因子が、別の対をなす光子の―電荷子と＋電荷子の電荷因子とクロス共有された状態を量子もつれと言う。
電荷因子は無限の速度を持つため距離は無関係であり、もつれ状態にある２つの光子を離しても一方の変化は他方にも瞬時に伝わる（量子テレポーテーション）。
その際もつれた光子に現れる変化が操作した光子の変化と逆方向となるのは、２つの系の安定のためである。
量子もつれは通常２対の粒子間でのもつれであるが、因子のもつれと考えるとN対の粒子のもつれがあっても不思議はない。
竜巻回転原子の各軌道には軌道面積の２倍の電子が配置され、お互いのスピンは逆スピン（アップとダウン）になっているが、これも２つの電子間で電荷因子がクロス共有されていることを示唆しており、一方の電子のスピンとは逆方向のスピンとすることで、全体としての系を安定にしているのだろう。