物質が静止している場合のエネルギーはE=mC²である。これはV=0の運動エネルギーと等価であり、静止時は重力エネルギー＝運動エネルギーとなっている。 質量mとは重力Gが１Gの時に測定した物質の相対質量である。

ここで宇宙区間（G=0）からブラックホール（最大重力S）に質量mの物体が落下するものと仮定する。
無重力(重力G＝０)状態における運動エネルギーはE=mC²/√(1－V²/C²)である。これに対し質量mの物質がブラックホールに落下する場合の重力エネルギーを考慮した式は、「運動エネルギーと重力エネルギーは、質量mに対し同時に同等に働く」と仮定するとE=mC²/√(1－V²/C²) (1－G²/S²)となる。 ここでSは、事象の地平面の重力S（シュバルツシルト面）で、光が脱出できない最大重力である。

この式にてV=0を当てはめ運動エネルギーを０にするとE=mC²/√(1－G²/S²)となり重力エネルギーの式となる。 さらに宇宙空間に静止し（V=０）、重力の働かない物体（G＝０）の条件を適用とするとE=mC²となり従来の静止時のエネルギーと同じになる。 また地上において速度0の物体に、重力G＝9.8m/s²を当てはめるとE=mC²/√(1－96.04/S²)となり宇宙空間に比べ大きくなる。 ただしSは極めて巨大なため殆どE≒mC²と考えて良い。

物体がブラックホールに落下し事象の地平面に達すると重力GはSに接近し分母が≒０となりエネルギーEは無限に近づく。 すなわち重力エネルギーと運動エネルギーは質量に対し各々別に作用する。
さらに「１章時間とは何か？」にて相対性理論を否定し、「２章運動エネルギー」と本章「３章位置エネルギー」で、その各々が異なることを述べた。
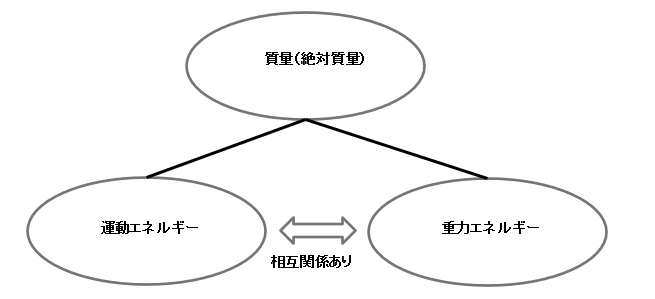
従って、本仮想物理では下図に示すように 「絶対質量、運動エネルギー、重力エネルギーは各々異なる物であり、質量とエネルギーは等価ではなくE=mC²は成り立たたない」と考える。
なお、絶対質量Ｍについては、次章で検討する。